
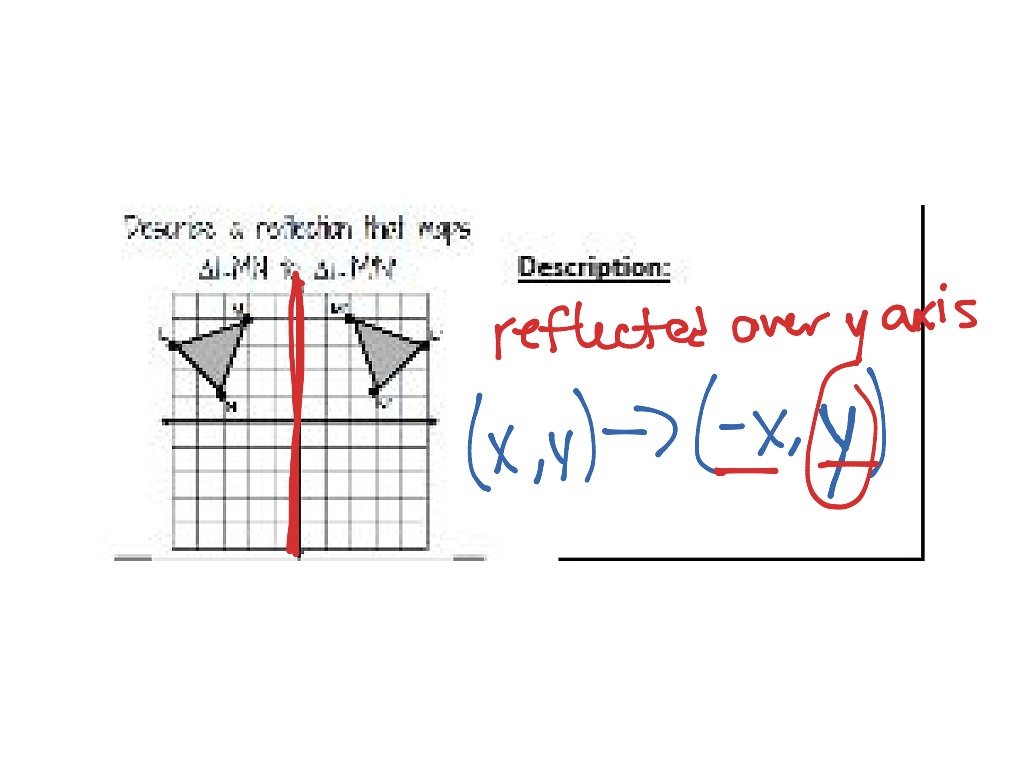
So the rule that we have to apply here is (x, y) -> (x, -y).īased on the rule given in step 1, we have to find the vertices of the reflected triangle A'B'C'. In geometry, a reflection is a type of transformation in which a shape or geometric figure is mirrored across a line or plane. Measure the same distance again on the other side and place a dot. A reflection point occurs when a figure is constructed around a single point known as the point of reflection or centre of the figure. The reflection of the point (x, y) across the line y x is (-y, -x). This will allow them the opportunity to identify what they did well, decide what they found interesting, and pinpoint where they need more support. The reflection of the point (x, y) across the line y x is (y, x). Here triangle is reflected about x - axis. Measure from the point to the mirror line (must hit the mirror line at a right angle) 2. Easily Add Math Reflection Time into Your Instruction Give your students time to step back and think about what they learned. Reflection Essay For Math Satisfactory Essays 1041 Words 5 Pages Open Document My thoughts in regards to the course up to this point are indifferent. If this triangle is reflected about x-axis, what will be the new vertices A', B' and C'?įirst we have to know the correct rule that we have to apply in this problem.
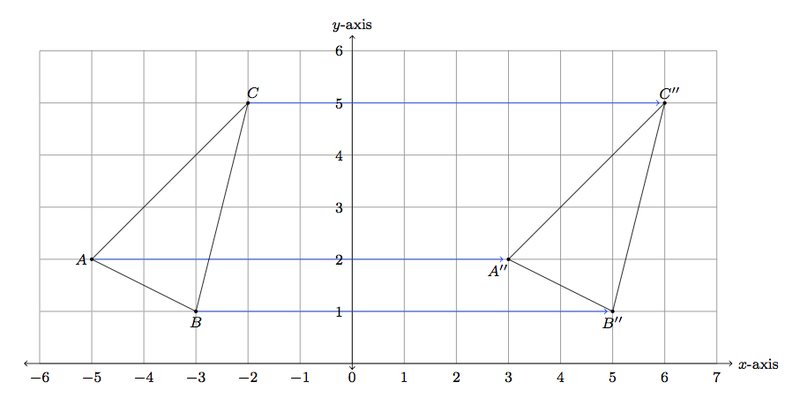
Let A ( -2, 1), B (2, 4) and (4, 2) be the three vertices of a triangle. Let us consider the following example to have better understanding of reflection.
Here the rule we have applied is (x, y) -> (x, -y). Lesson Powerpoint presentation for reflection in a diagonal line Reflection of a shape in a 45 degree line, two examples and two worksheets to print out. Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection -transformation of a figure.įor example, if we are going to make reflection transformation of the point (2,3) about x-axis, after transformation, the point would be (2,-3).


 0 kommentar(er)
0 kommentar(er)
